2019年人教版数学高中一年级上学期综合测试卷二
1、选择题:
1.已知集合![]() ,
,![]() ,且
,且![]() ,则
,则![]() 的值为 ( )
的值为 ( )
A.1 B.—1 C.1或—1 D.1或—1或0
2.函数![]() 的概念域为( )
的概念域为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3. 已知集合![]() ,则M∩N=( )
,则M∩N=( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
4.若![]() 为全集,下面三个命题中真命题的个数是( )
为全集,下面三个命题中真命题的个数是( )
(1)若![]()
(2)若![]()
(3)若![]()
A.![]() 个 B.
个 B.![]() 个 C.
个 C.![]() 个 D.
个 D.![]() 个
个
5.不等式![]() 的解集为R,则
的解集为R,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.![]()
![]() 则
则![]() 为( )
为( )
A.![]() B.
B.![]() 或
或![]() C.0D. 2
C.0D. 2
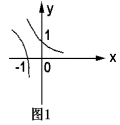 7.在同一坐标系内作出的两个函数图像图1所示,则这两个函数为( )
7.在同一坐标系内作出的两个函数图像图1所示,则这两个函数为( )
A、y=ax 和y=loga B、y=ax 和y=logax-1
C、y=a-x 和y=logax-1 D、y=a-x 和y=loga
8.如图,U是全集,M、P、S是U的3个子集,则阴影部分所表示的集合是 ( )
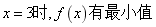 A、
A、 ![]() B、
B、 ![]()
C、 ![]() D、
D、 ![]()
9.函数f= x2+2x+2在区间上递减,则a的取值范围是
A. ![]() B.
B. ![]() C. D.
C. D.![]()
10.![]() ,
,![]() ,则A∩B=( )
,则A∩B=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.下列所给4个图象中,与所给3件事吻合最好的顺序为( )
(1)我离开家不久,发现自己把作业本忘在家了,于是立刻返回家取了作业本再上学;
(2)我骑着车一路以常速行驶,只不过在途中遇见一次交通堵塞,耽搁了一些时间;
(3)我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速、

A、(1)(2)(4) B、(4)(2)(3) C、(4)(1)(3) D、(4)(1)(2)
12.函数![]() 在区间
在区间![]() 上单调递增,则实数a的取值范围( )
上单调递增,则实数a的取值范围( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2、填空题:
13.设集合![]() ,B={1,2,3,4},则
,B={1,2,3,4},则![]() =_______.
=_______.
14.已知集合A={![]() ,
,![]() ,2},B={2,
,2},B={2,![]() ,2
,2![]() }且,
}且,![]() =
=![]() ,则
,则![]() =__________ __________.
=__________ __________.
15.函数![]() 在区间
在区间![]() 上递减,则实数
上递减,则实数![]() 的取值范围是___________
的取值范围是___________
16.对于函数![]() ,概念域为
,概念域为![]() ,以下命题正确的是(只须求写出命题的序号)__________
,以下命题正确的是(只须求写出命题的序号)__________
①若![]() ,则
,则![]() 是
是![]() 上的偶函数;
上的偶函数;
②若对于![]() ,都有
,都有![]() ,则
,则![]() 是
是![]() 上的奇函数;
上的奇函数;
③若函数![]() 在
在![]() 上具备单调性且
上具备单调性且![]() 则
则![]() 是
是![]() 上的递减函数;
上的递减函数;
④若![]() ,则
,则![]() 是
是![]() 上的递增函数。
上的递增函数。
17. 已知:集合![]() ,集合
,集合![]() ,
,
求![]()
18. (本题满分12分)设集合![]() B
B![]() ,
,
分别就下列条件,求实数a的取值范围:
①![]() ; ②
; ②![]()
19.已知函数![]() 的概念域为R,求实数
的概念域为R,求实数![]() 的范围.
的范围.
20.已知函数![]() ,
,
(1)证明函数![]() 的单调性;
的单调性;
(2)求函数![]() 的最小值和最大值。
的最小值和最大值。
21. (本题满分12分)已知函数![]() ,若
,若![]() 在区间
在区间![]() 上有最大值
上有最大值![]() ,最小值
,最小值![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() 在
在![]() 上是单调函数,求
上是单调函数,求![]() 的取值范围.
的取值范围.
22.(本小题满分12分)
有甲,乙两家健身中心,两家设施和服务都相当,但收费方法不同.甲中心每小时5元;乙中心按月计费,一个月中30小时以内(含30小时)90元,超越30小时的部分每小时2元.某人筹备下个月从这两家里选择一家进行健身活动,其活动时间不少于15小时,也低于40小时。
(1)设在甲中心健身![]() 小时的收费为
小时的收费为![]() 元
元![]() ,在乙中心健身活动
,在乙中心健身活动![]() 小时的收费为
小时的收费为![]() 元。试求
元。试求![]() 和
和![]() ;
;
(2)问:选择哪家比较划算?为何?
参考答案
1、选择题:1-5:DADDC 6-10:CDCBB 11-12:DB
2、填空题:13. ![]() 14. 0或
14. 0或![]() 15.__________
15.__________![]() __________ 16. ______________________________
__________ 16. ______________________________
3、解答卷:
17、解:![]() 是函数
是函数![]() 的概念域
的概念域 ![]()
解得 ![]() 即
即![]()
![]() 是函数
是函数![]() 的值域
的值域
解得 ![]() 即
即![]()
![]()
18、解:(1)∵![]() ∴
∴![]() 或
或![]() 即
即![]() 或
或![]()
(2)∵![]() ∴
∴![]() ∴
∴![]() 或
或![]() 即
即![]() 或
或![]()
19、解:![]()
20、(1)设![]() ,则
,则![]()
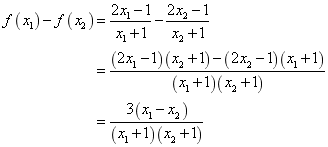
![]() ∴
∴ ![]()
∴ ![]() ∴
∴ ![]() 上是增函数
上是增函数
(2)由(1)可知![]() 上是增函数,
上是增函数,
∴ 当![]()
![]() 当
当![]()
21、(1)由![]() ,
,![]() 可知,
可知,![]() 在区间
在区间![]() 单调递增,
单调递增,
即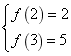 解得:
解得:![]() ;
;
(2)![]() 在
在![]() 上是单调函数,仅需
上是单调函数,仅需
![]() 或
或![]()
![]()
![]() 或
或![]()
22、解:(1)![]() ,
,![]() ,
,
![]() ;
;
(2)当5x=90时,x=18,
即当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
∴当![]() 时,选甲家比较划算;当
时,选甲家比较划算;当![]() 时,两家一样划算;
时,两家一样划算;
当![]() 时,选乙家比较划算.
时,选乙家比较划算.







